Gerando Equações e gráficos

 

Esse applet é uma ferramenta interativa projetada para criar equações matemáticas a partir de listas de sequências numéricas. O applet é ideal para estudantes, educadores e entusiastas da matemática que desejam explorar a relação entre sequências e equações de forma visual e prática.

Construção do applet passo a passo

Acessando o geogebra online: GeoGebra Classic

1 - Na caixa de entrada digite:

Sequência("a_{"i"}=RandomBetween(1,5)",i,1,4)

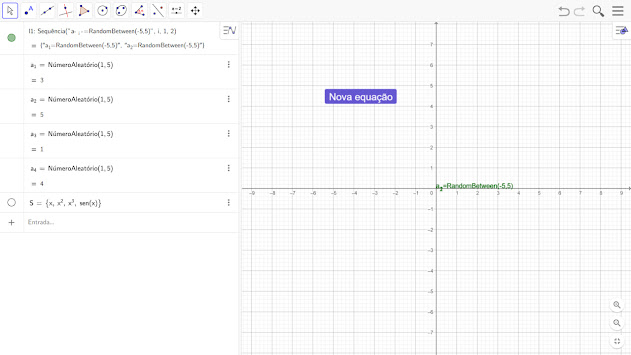
2 - Executar a sequência lista 1, ou seja l1

Na caixa de entrada digite: Execultar(l1)

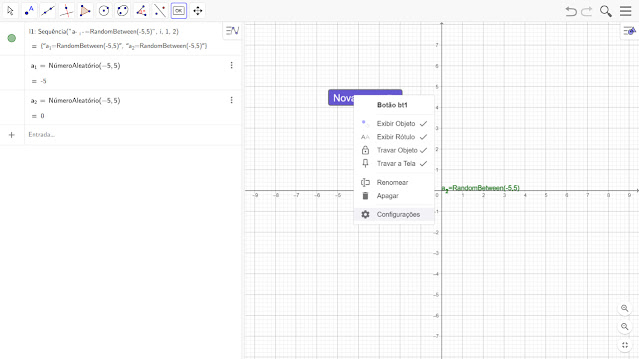
3 - Com a ferramenta botão criaremos o "Nova Equação".

Com o botão direito do mouse, clicando no botão, em configurações, teremos:

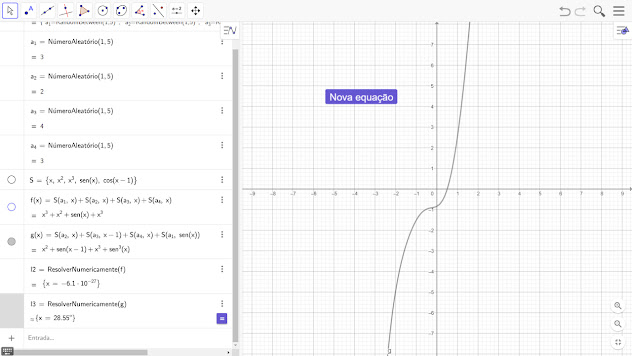
4 - Dentro desse espaço digite:

Executar(Sequência("a_{"i"}=RandomBetween(1,5)",i,1,4))

5 - Digite a seguinte sequência na caixa de entrada:

S={x,x^(2),x^(3),sen(x)}

6 - Digitamos na caixa de entrada S(a_1), no momento teremos o seguinte resultado:

f(x) = S(a_1, x)

= sen(x)

Veja que a_1 = 4, corresponde ao quarto elemento da Sequência S, que nesse caso é:

S= {x, x^2, x^3, sen(x)}

7 - Ao pressionarmos o botão "Nova Equação" temos:

Temos no momento a_1 = 2, e o segundo elemento da sequência S = {x, x^2, x^3, sen(x)) é: x^2

8 - Vamos acrescentar um novo elemento a tabela S, porque vemos que estão sendo lançados números aleatórios que vão de 1 a 5, isso é importante pra não acontecer erros;

S={x,x^(2),x^(3),sen(x),cos(x-1)}

9 - Poderemos montar a nossa função f(x) de diversas maneiras vamos escolher algumas:

Pode ser assim:

f(x)=S(a_{1},x) + S(a_{2},x)+ S(a_{3},x)+S(a_{4},x)

Graficamente temos:

Pode ser assim, também:

g(x)=S(a_{2},x)+S(a_{3},x-1)+S(a_{4},x)+S(a_{1},sen(x))

Graficamente temos:

10 - Ao pressionarmos o botão "Nova equação" teremos sempre uma equação gerada a partir das sequências que criamos, veja:

 

11 - Usando o comando: ResolverNumericamente, assim:

Escolhendo a função f. Poderemos assim obter a raiz numérica dessa equação:

12 - Podemos escolher a função g(x), e usar o mesmo comando:

O objetivo desse exercício é fornecer uma plataforma acessível e intuitiva para a exploração de sequências e suas representações matemáticas. Ao facilitar a criação e análise de equações a partir de sequências numéricas, o applet ajuda a aprofundar o entendimento dos usuários sobre padrões matemáticos e suas aplicações.

▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️

Os applets exclusivos estão disponíveis para assinantes do youtube

Assinar: https://www.youtube.com/channel/UCf-nkL6ijeHHT6bIJMF1ksQ/join

▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️▪️

REFERÊNCIAS

01 - APRENDENDO GEOGEBRA (https://amzn.to/3LHoU4T)

02 - MATEMÁTICA DINÂMICA (https://amzn.to/3SndyGH)

03 - APENDIZADO DINÂMICO USANDO O GEOGEBRA (https://amzn.to/4d0THpi)

04 - GEOGEBRA: SOLUÇÕES E PRÁTICAS NA GEOMETRIA ANALÍTICA (https://amzn.to/4fpircj)

05 - GEOGEBRA: ANIMAÇÕES GEOMÉTRICAS (https://amzn.to/4c3rVHd)

06 - OBJETOS DE APRENDIZAGEM NO GEOGEBRA (https://amzn.to/3LLjqpS)

07 - EXPLORANDO A PROPORÇÃO PERFEITA (https://amzn.to/3yi1foq)

08 - EXPOSIÇÃO DE EXERCÍCIOS USANDO O GEOGEBRA (https://amzn.to/3WSi03f)

09 - INTEGRAIS RESOLVIDAS (https://amzn.to/46siH68)

10 - EXPLORANDO A MATEMÁTICA DE FORMA INTERATIVA (9o ano) (https://amzn.to/3WnNxZg)

11 - MÉTODOS NUMÉRICOS: PONTO FIXO COM MATLAB E PHYTON: https://amzn.to/4d1glO6

12 - QUESTÕES DE VESTIBULAR: TEORIA E PRÁTICA (https://amzn.to/3Wt4EZJ)

13 - APRENDENDO GEOGEBRA: PROPRIEDADES DE FIGURAS GEOMÉTRICAS E PLANAS (https://amzn.to/3LIzyIr)

14 - MATEMÁTICA INTERATIVA: EXPLORANDO CONCEITOS COM O GEOGEBRA (https://amzn.to/4frHb3U)

15 - GEOMETRIA ESPACIAL: UMA BORDAGEM DINÂMICA USANDO O GEOGEBRA (https://amzn.to/4fCE35l)

16 - MÉTODO DA BISSECÇÃO: Uma abordagem dinâmica usando o Maplesoft e o Geogebra. https://amzn.to/4dt3ap4

17 - Métodos Numéricos: Ponto fixo com MATLAB e Python: https://amzn.to/3Wt1i8Q

18 - Método de Newton-Raphson: Uma abordagem dinâmica usando o Maplesoft e o Geogebra: https://amzn.to/3LUOG5O

19 - MATLAB: Métodos Numéricos e Gráficos: https://amzn.to/4cw0ZAt

20 - Matlab: numerical and graphical methods: https://amzn.to/4fAztEr